两数之和和三数之和

两数之和

输入一个递增排序的数组和一个数字s，在数组中查找两个数，使得它们的和正好是s。如果有多对数字的和等于s，则输出任意一对即可。

对撞双指针

在数组的左右各有一个指针，向中间遍历。指针指向的两数和为s，则s=nums[i]+nums[j]，判断s和target的大小：

s > target, 则右指针向左移, j--
s < target, 则左指针向右移, i++
s = target, 返回[nums[i],nums[j]]

代码实现

/**
 * @param {number[]} nums
 * @param {number} target
 * @return {number[]}
 */
var twoSum = function (nums, target) {
  let i = 0,
    j = nums.length - 1
  while (i < j) {
    s = nums[i] + nums[j]
    if (s > target) j--
    else if (s < target) i++
    else return [nums[i], nums[j]]
  }
}

使用Map查找

我们先将数组中的元素item存储到Map中，然后在使用map[target-item]即可查看是否存在与item相匹配的数。

代码实现：

var twoSum = function (nums, target) {
  let map = {}
  nums.forEach((item) => (map[item] = item))
  for (item of nums) {
    if (map[target - item]) return [item, map[target - item]]
  }
}

运行时间和内存消耗对比，先运行的双指针，所以上边是使用Map，下边是双指针。

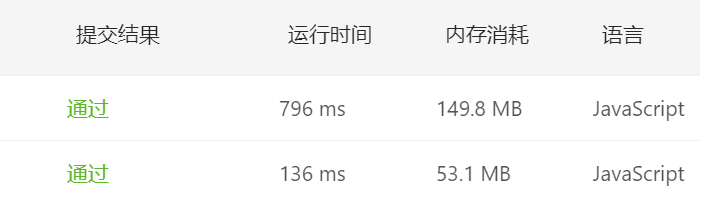
分析：

从时间复杂度来说，Map很明显花费了更多的时间，先遍历一遍元素生成Map，再遍历一遍访问Map，时间复杂度为O(2n)；双指针法两个指针向中间遍历，只需要遍历一次元素，时间复杂度为O(n)。
空间复杂度上来看，使用Map会额外创建O(n)的空间；双指针法创建两个指针，空间复杂度为O(2n)。

三数之和

有一个整数数组 nums，判断 nums 中是否存在三个元素 a，b，c 的和为0，找出所有符合条件且不重复的三元组。

双指针法

暴力解题需要三重循环，时间复杂度为O(n³)，而我们在代码中应该尽量避免这么多层循环，除非每层的数据特别少。

两数之和，我们使用了双指针法，将O(n²)的时间复杂度降低到了O(n)，在这个问题里，我们可以使用遍历+双指针，将原本O(n³)的时间复杂度降低到O(n²)。

双指针法的思路如下，先将数组排序，之后遍历元素，对于每个元素nums[i]，在nums[i]~nums[nums.length-1]中使用双指针遍历，则s = nums[i] + nums[l] + nums[r]，然后判断s是否等于0。

我们之所以将数组排序，是因为可以得到一个好的跳出循环条件：**排序后，元素是升序的，当nums[i]大于0的时候，后边的元素也肯定是大于0，s大于0，则可以跳出循环。**排序的时间复杂度为O(nLogn)，时间复杂度并不算高，当数据量很大的情况，肯定换来提前结束循环肯定是稳赚不赔。

/**
 * @param {number[]} nums
 * @return {number[][]}
 */
var threeSum = function (nums) {
  let res = []
  if (nums.length < 3) return []
  nums.sort((a, b) => a - b)
  for (let i = 0; i < nums.length; i++) {
    if (nums[i] > 0) break
    if (i > 0 && nums[i] == nums[i - 1]) continue
    let l = i + 1,
      r = nums.length - 1
    while (l < r) {
      const s = nums[i] + nums[l] + nums[r]
      if (s == 0) {
        res.push([nums[i], nums[l], nums[r]])
        while (l < r && nums[l] == nums[l + 1]) l++
        while (l < r && nums[r] == nums[r - 1]) r--
        l++
        r--
      } else if (s < 0) l++
      else if (s > 0) r--
    }
  }
  return res
}

时间复杂度O(n²)，nums[i]遍历O(n)，nums[l] + nums[r]遍历O(n)，越到后边，每层遍历的次数越少，总的遍历过程呈现一个倒三角的过程。